~ t検定で仕事に差をつけよう!~

こんにちは!走る園児の運動会にようこそ。
今回は「データの検定」という、統計の中でも超・実務に役立つテクニックを、例題を使ってやさしく解説していきます!
◆ そもそも「検定」ってなに?
「検定」とは、データを使って“仮説が正しいかどうか”を判断する方法です。
たとえば…
新しい製造ラインは、旧ラインよりも製品の精度が高いって言えるのかな?
そんなときに「検定」の出番!
◆ 今回の事例:新旧2つのラインの精度比較
ある技術者Aさんが、以下のようなデータをとってきました。
| 測定回 | 旧ライン(精度) | 新ライン(精度) |
|---|---|---|
| 1 | 10.1 | 10.3 |
| 2 | 9.8 | 10.2 |
| 3 | 10.0 | 10.4 |
| 4 | 10.2 | 10.5 |
| 5 | 9.9 | 10.1 |
Aさんの仮説:「新ラインの方が精度が良い!」
この仮説が統計的に正しいかを「t検定」で調べます。
◆ ステップ①:t検定って何?
「t検定」は、2つのグループの平均に差があるかどうかを判断する方法です。
今回は「対応のあるt検定」(同じ製品を旧ラインと新ラインで測った)を使います。
◆ ステップ②:実際に計算してみよう!
1. 差を求める
旧ラインと新ラインの差(新 − 旧)を計算します:
| 測定回 | 新−旧(差) |
|---|---|
| 1 | 10.3 – 10.1 = 0.2 |
| 2 | 10.2 – 9.8 = 0.4 |
| 3 | 10.4 – 10.0 = 0.4 |
| 4 | 10.5 – 10.2 = 0.3 |
| 5 | 10.1 – 9.9 = 0.2 |
差の平均=(0.2 + 0.4 + 0.4 + 0.3 + 0.2)/5 = 0.3
差の標準偏差 ≒ 0.083(手計算でやってもいいですが、ExcelでもOK!)
2. t値を計算する
🧩 各パーツの意味
| 記号 | 意味(簡単に) | 詳しい意味 |
|---|---|---|
| dˉ | 差の平均値 | 各ペアごとの差(新−旧)の平均 |
| s | 差の標準偏差(ばらつき) | 差の散らばりの大きさを表す指標 |
| n | データの個数 | 差の数(ペアの数) |
| データ数の平方根 | 平均のばらつきを調整するために必要 | |
| s/ √n | 標準誤差(standard error) | 平均値の信頼性の目安。ばらつきの調整版 |
🎯 t値の意味:
つまり、
「差の平均が、ばらつきに対してどれだけ大きいか」を示している!
t値が大きければ大きいほど、
「差が偶然とは思えない → 有意な差がある」と判断されます!
📌 まとめ(初心者向け解釈)
| t値が小さい | 差は偶然っぽい(有意差なし) |
|---|---|
| t値が大きい | 差は本物っぽい(有意な差がある!) |
n = 5(データ数)
t = 0.3 / (0.083 / √5) ≒ 0.3 / 0.037 ≒ 8.11
◆ ステップ③:t値から結論を出す!
自由度 = n – 1 = 4。
有意水準(α)を 5% とすると、t分布表の臨界値 ≒ 2.776
t = 8.11 > 2.776 なので…
💡 「新ラインの方が精度が高い」という仮説は統計的に有意!
◆ まとめ:t検定のキモはココ!
「差がたまたまか、本物か?」を見極めるのが検定!
t検定では「平均の差」が有意かどうかを判断する
実データに基づいて、ちゃんと「言える根拠」ができる!
🛠 おまけ:Excelでt検定をやってみよう!
これで一発です!自動でp値が出て、p < 0.05なら有意差あり!

気になったこと・もっと詳しく知りたい検定方法があれば、
コメントやメッセージで教えてね!



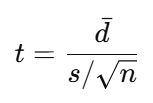



コメント